Abstract: SuGaR and 2D Gaussian Splatting address the fundamental limitation of 3D Gaussian Splatting in producing structured geometric representations. SuGaR introduces surface alignment regularization to enable rapid mesh extraction from existing 3DGS representations, while 2DGS reformulates Gaussian primitives as oriented 2D disks to achieve inherent surface modeling. Both methods enable mesh extraction in minutes compared to hours required by neural SDF approaches.
Introduction: The Geometric Representation Problem
3D Gaussian Splatting [3] revolutionized real-time novel view synthesis by representing scenes as collections of 3D Gaussian primitives. Each Gaussian is parameterized by its mean position μ, covariance matrix Σ (encoded as scaling and rotation), opacity α, and view-dependent color coefficients. The rasterization-based rendering achieves real-time performance by projecting 3D Gaussians into image space and compositing them using alpha blending.
Note
More on 3DGS can be found here
However, this representation presents a critical limitation: the optimized Gaussians form an unstructured point cloud that does not correspond to the scene’s actual surface geometry. After optimization, Gaussians are distributed throughout the volumetric space rather than concentrated on surfaces, making explicit mesh extraction challenging.
This geometric inconsistency creates a significant gap in practical applications. While 3DGS excels at photorealistic rendering, it cannot provide the structured mesh representations required for traditional computer graphics workflows including geometric editing, physics simulation, and content authoring tools.
Problem Formulation
Consider a 3DGS scene represented by N Gaussian primitives , where each Gaussian Gᵢ is defined by parameters (). The volume density function at any point is computed as:
 In an ideal surface representation, this density function would exhibit sharp transitions at surface boundaries. However, standard 3DGS optimization using photometric losses alone does not constrain Gaussians to align with geometric surfaces, resulting in:
In an ideal surface representation, this density function would exhibit sharp transitions at surface boundaries. However, standard 3DGS optimization using photometric losses alone does not constrain Gaussians to align with geometric surfaces, resulting in:
- Volumetric distribution: Gaussians are scattered throughout 3D space rather than concentrated on surfaces
- Geometric inconsistency: The implicit surface defined by density level sets does not correspond to the scene’s true geometry
- Multi-view artifacts: Rendered geometry appears inconsistent when viewed from different angles
SuGaR: Surface-Aligned Gaussian Regularization [1]
Theoretical Foundation
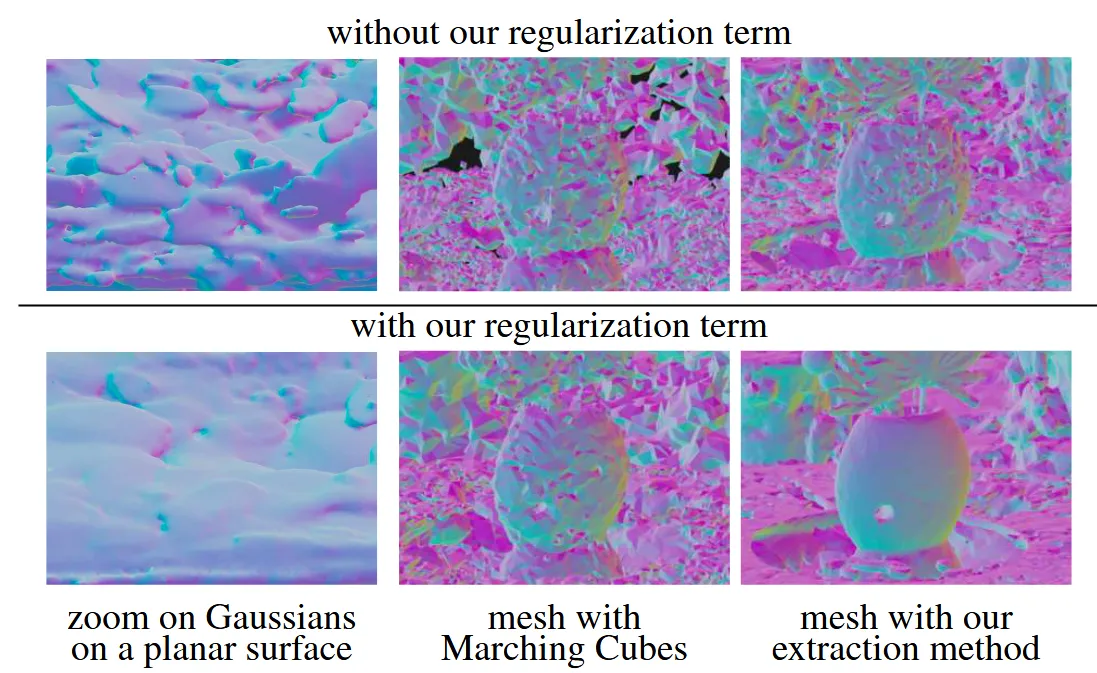
SuGaR addresses the surface alignment problem through regularization during 3DGS optimization. The method introduces additional constraints that encourage Gaussians to:
- Flatten against surfaces (minimize thickness in the surface-normal direction)
- Become binary in opacity (either fully opaque or transparent)
- Align with the underlying scene geometry
The approach builds on the observation that for surface-aligned Gaussians with minimal overlap, the contribution of the nearest Gaussian to the density at any surface point p dominates other contributions.
SDF-Based Regularization Term
Rather than directly regularizing the density function, SuGaR employs a Signed Distance Function (SDF) formulation. For a Gaussian Gᵢ with center and surface normal , the ideal SDF represents level sets as planes:
The regularization loss minimizes the L2 difference between this ideal SDF and an estimated SDF derived from the current Gaussian configuration:
where points p are sampled according to the Gaussian distribution to ensure high gradient regions are adequately represented.
Efficient SDF Estimation
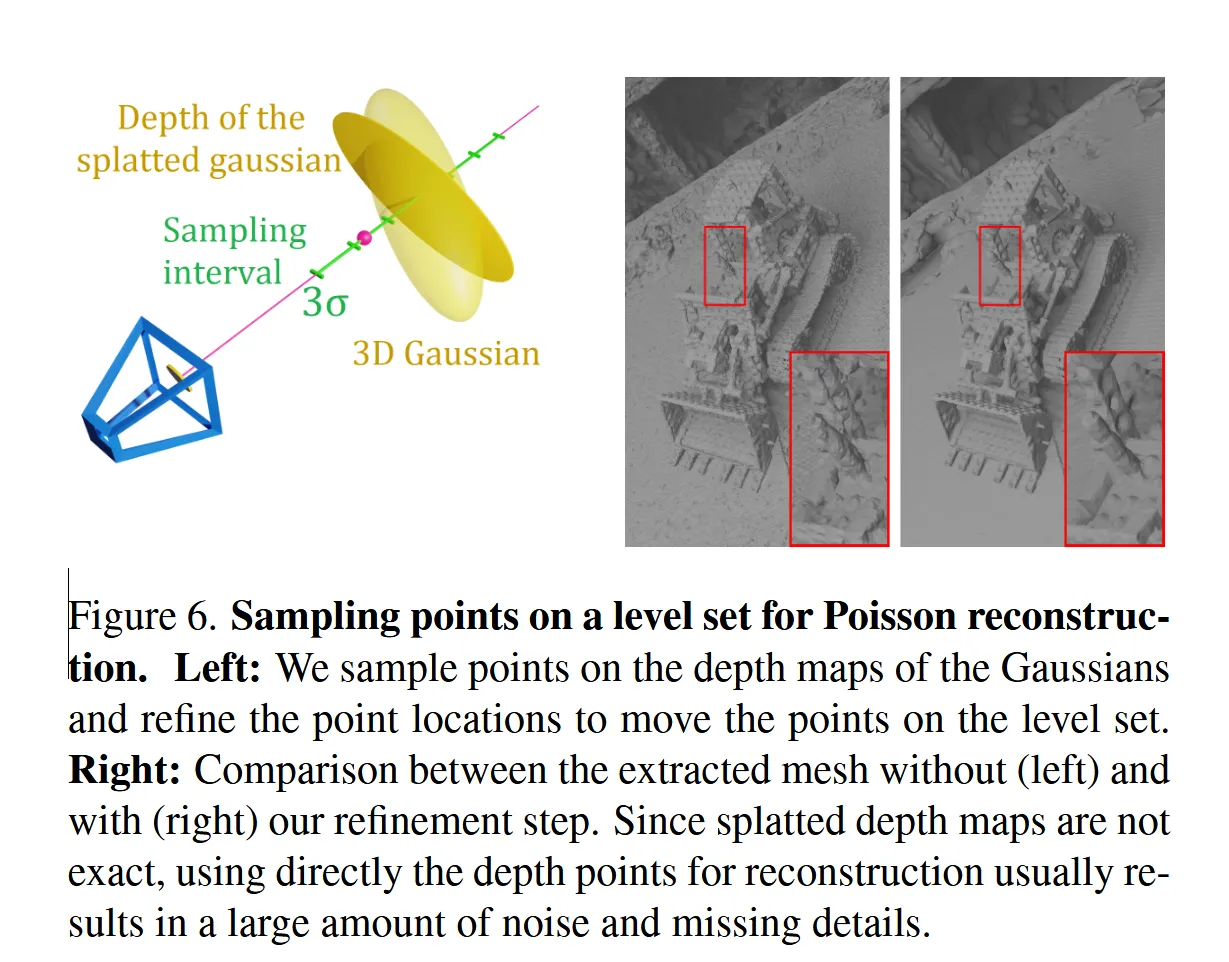
Computing the SDF efficiently during optimization requires careful implementation. SuGaR leverages depth maps rendered from training viewpoints using the differentiable splatting rasterizer. For each pixel ray, the method samples points along the viewing direction and evaluates the density function to estimate SDF values through finite differences.
The normal consistency term further improves surface quality by aligning SDF gradients:
Mesh Extraction via Poisson Reconstruction
Once Gaussians are regularized for surface alignment, mesh extraction becomes computationally tractable. The process involves:
Level Set Sampling: Points on the λ-level set of the density function are sampled by:
- Random pixel sampling from rendered depth maps
- Ray marching along viewing directions to find density intersections
- Linear interpolation to locate precise level set points
- Normal computation from SDF gradients
Poisson Surface Reconstruction [4]: The sampled points with normals serve as input to the Poisson reconstruction algorithm, which solves the Poisson equation ∇²χ = ∇ · V where V is the vector field defined by the oriented points.
This approach scales efficiently to millions of Gaussians, extracting meshes in 5-10 minutes compared to 24-48 hours required by neural SDF methods.
Refinement Through Gaussian-Mesh Binding
The optional refinement stage introduces a novel parameterization that binds Gaussians directly to mesh triangles. For each triangle T with vertices (v₀, v₁, v₂), a set of n Gaussians are instantiated with positions defined by barycentric coordinates:
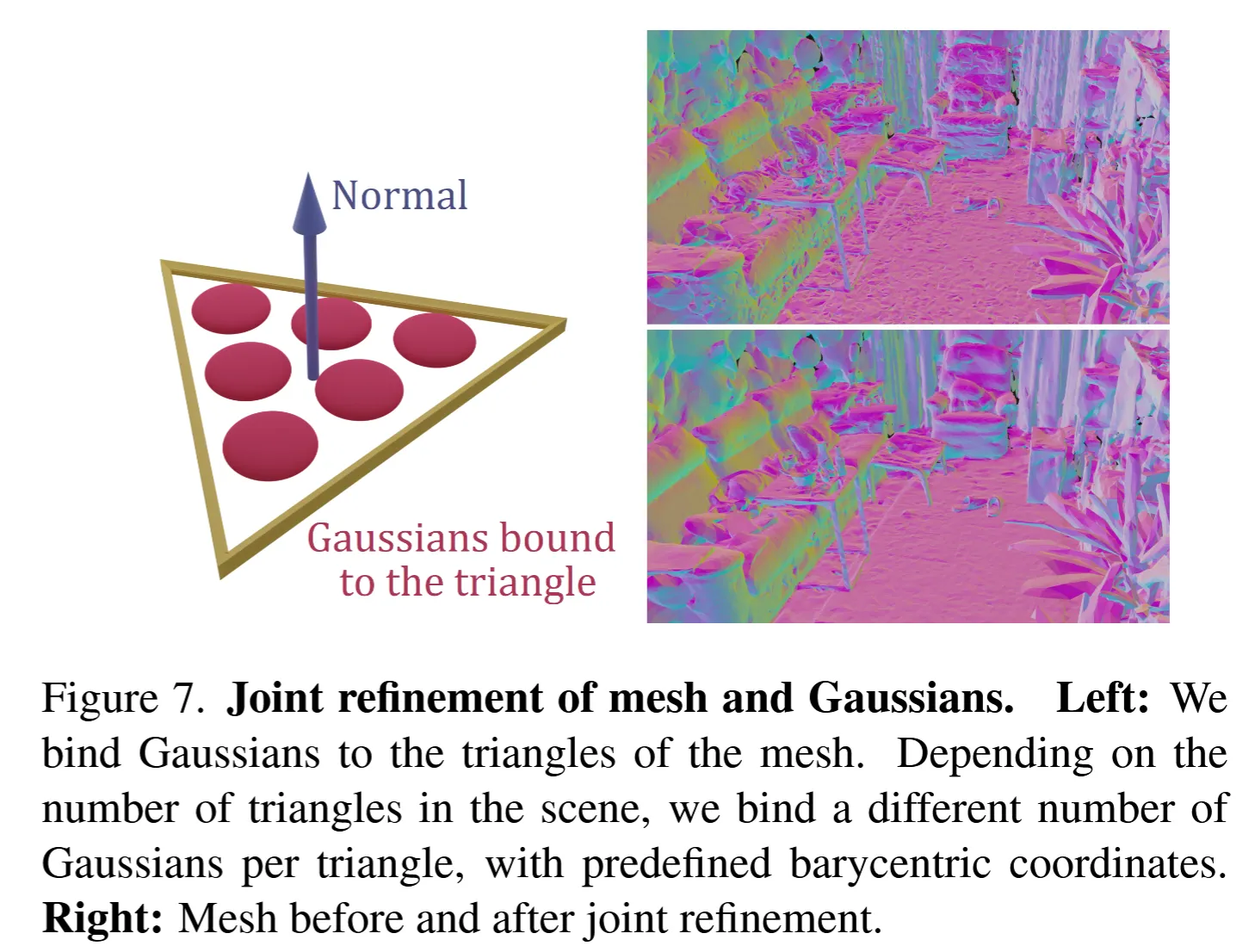
The Gaussian orientation is constrained to the triangle plane through a 2D rotation parameterization. Instead of optimizing a full quaternion, the method optimizes a complex number z = x + iy encoding in-plane rotation.
Joint optimization of mesh vertices and Gaussian parameters enables high-quality rendering while maintaining editability. Mesh deformations automatically propagate to bound Gaussians, preserving rendering fidelity during geometric editing operations.
2D Gaussian Splatting: Reformulating Gaussian Primitives [2]
Fundamental Representation Change
2DGS addresses the surface modeling problem by fundamentally changing the Gaussian primitive from 3D ellipsoids to 2D oriented disks. Each 2D Gaussian is parameterized by:
- Center point
- Two orthogonal tangent vectors defining the local coordinate system
- Scaling factors controlling disk extent
- Standard opacity and color coefficients
The 2D Gaussian value at local coordinates (u, v) within the disk plane is evaluated as:
This representation intrinsically models surfaces since Gaussians have zero thickness perpendicular to their orientation plane.
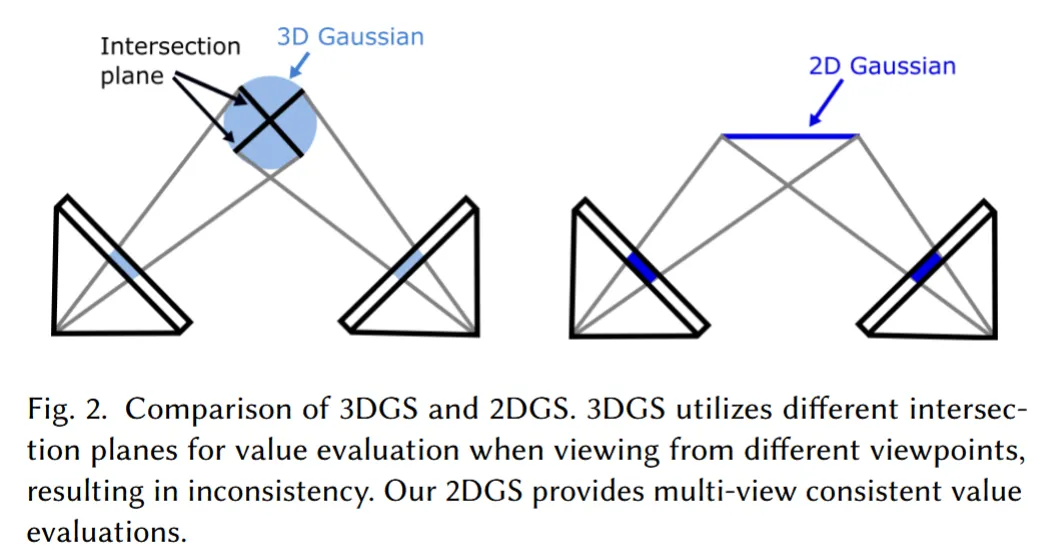
Perspective-Accurate Ray-Splat Intersection
A critical technical contribution of 2DGS is perspective-accurate rendering that overcomes limitations of 3DGS’s affine approximation. The method computes exact intersections between viewing rays and 2D Gaussian disks.
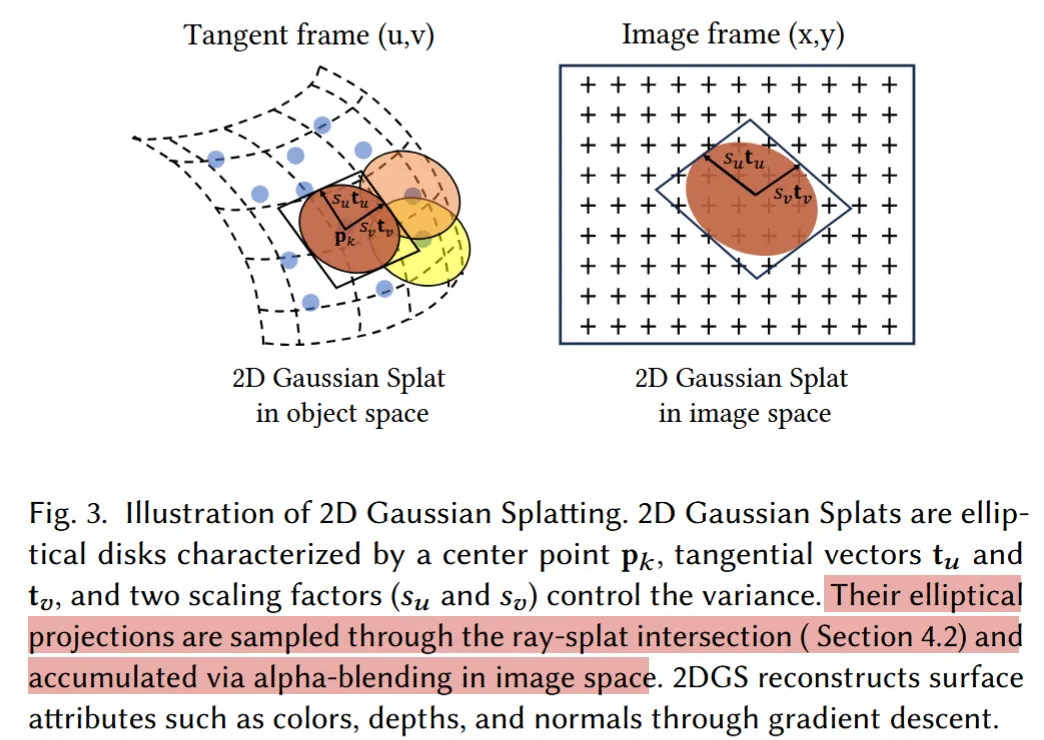
This geometric approach ensures accurate rendering from arbitrary viewpoints, including grazing angles where 2D disks appear as lines in screen space.
Regularization for Geometric Consistency
2DGS introduces two regularization terms essential for high-quality reconstruction:
Depth Distortion Regularization: This term concentrates 2D primitives along viewing rays by minimizing the variance of intersection depths:
where wᵢ are rendering weights, zᵢ are intersection depths.
Normal Consistency Regularization: This constraint aligns 2D Gaussian orientations with surface normals estimated from depth gradients:
where n_i is normal of gaussian oriented toward camera, N is surface normal from depth map.
Mesh Extraction Through TSDF Fusion
2DGS employs Truncated Signed Distance Function (TSDF) fusion for mesh extraction. The method renders depth maps from training viewpoints, where depth values correspond to ray-splat intersection distances. These depth maps are fused using volumetric integration to produce a consistent 3D reconstruction.
The surface is extracted at the median depth along each ray, defined as the depth where accumulated opacity reaches 0.5. This approach proves more robust than expected depth computation, which is sensitive to outlier contributions.
Comparative Analysis


Computational Performance
| Method | Training Time | Memory Usage | Rendering Speed |
|---|---|---|---|
| Neural SDFs | 24-48 hours | High | Slow (seconds) |
| SuGaR | ~1 hr | Medium | Real-time |
| 2DGS | 15-20 minutes | Medium | Real-time |
Geometric Accuracy Metrics
Quantitative evaluation on standard datasets demonstrates significant improvements in geometric reconstruction quality:
Chamfer Distance: Both methods achieve 2-3x lower Chamfer distance compared to standard 3DGS mesh extraction attempts.
Normal Consistency: 2DGS shows superior normal consistency metrics due to its intrinsic surface representation.
Multi-view Consistency: 2DGS demonstrates better geometric consistency across different viewpoints due to perspective-accurate rendering.
Failure Modes and Limitations
Both methods exhibit specific limitations that constrain their applicability:
Semi-transparent Materials: Neither method handles materials with complex light transport (glass, water, participating media) effectively, as both assume surface-based representations.
Highly Specular Surfaces: Strong specular reflections can interfere with surface alignment constraints, leading to artifacts in mirror-like materials.
Sparse View Coverage: Both methods require adequate view coverage for reliable surface reconstruction. Sparse input (fewer than 20-30 views) may result in incomplete or inaccurate geometry.
Implementation Considerations
Hardware Requirements
Optimal performance requires NVIDIA GPUs with substantial memory:
- Minimum: RTX 3080 (10GB VRAM)
- Recommended: RTX 4080 (16GB VRAM)
- Optimal: RTX 4090 (24GB VRAM)
Memory requirements scale with scene complexity and desired mesh resolution. High-resolution mesh extraction may require 16GB+ VRAM.
Software Dependencies
Both implementations build upon the original 3DGS codebase with additional dependencies:
SuGaR:
- PyTorch 1.12+
- PyTorch3D for mesh operations
- Open3D for Poisson reconstruction
- CUDA 11.8+ for custom kernels
2DGS:
- Custom CUDA kernels for ray-splat intersection
- Modified splatting rasterizer
- TSDF fusion implementation
Parameter Selection
Critical hyperparameters require careful tuning:
SuGaR:
- Surface alignment weight: 0.01-0.1
- Level set value λ: 0.1-0.5
- Poisson reconstruction depth: 8-12
2DGS:
- Depth distortion weight: 0.01-0.05
- Normal consistency weight: 0.01-0.1
- TSDF truncation distance: 2-5 voxels
Applications and Use Cases
Digital Content Creation
Architectural Visualization: 2DGS provides geometrically accurate reconstructions suitable for architectural documentation and renovation planning.
Film and VFX: SuGaR’s editability enables integration of captured environments with computer graphics elements in post-production workflows.
Game Development: Both methods enable rapid environment capture for realistic game assets, with SuGaR offering superior editing capabilities for level design.
Scientific and Industrial Applications
Cultural Heritage: High-fidelity 3D documentation of artifacts and archaeological sites with geometric accuracy for measurement and analysis.
Quality Control: Industrial inspection applications requiring precise geometric measurements alongside photorealistic visualization.
Digital Twins: Creating accurate virtual replicas of physical environments for simulation and monitoring applications.
Current Research Directions
Dynamic Scene Handling
Recent work investigates extending both methods to handle temporal variations:
- Time-dependent Gaussian parameters for dynamic objects
- Temporal consistency constraints for moving geometry
- Real-time capture and reconstruction pipelines
Material Property Estimation
Integration with physically-based rendering models:
- BRDF parameter estimation from multi-view captures
- Relighting capabilities for extracted meshes
- Handling of complex material properties (subsurface scattering, fluorescence)
Scalability Improvements
Ongoing research addresses computational scalability:
- Hierarchical representations for large-scale scenes
- Streaming algorithms for real-time processing
- Distributed computation for massive datasets
Conclusion
SuGaR and 2DGS represent significant advances in bridging the gap between neural rendering and structured geometric representations. SuGaR provides an efficient retrofit solution for existing 3DGS captures, enabling mesh extraction and editing through surface alignment regularization. 2DGS offers a more fundamental approach with intrinsic surface modeling through 2D oriented Gaussian disks.
Both methods achieve mesh extraction orders of magnitude faster than neural SDF approaches while maintaining high geometric accuracy. The choice between methods depends on specific application requirements: SuGaR for maximum editability and compatibility with existing 3DGS workflows, 2DGS for geometric accuracy and consistency from the outset.
These developments mark the maturation of Gaussian Splatting from a pure rendering technique into a complete 3D reconstruction and content creation pipeline. As the methods continue to evolve, they promise to democratize high-quality 3D content creation and enable new applications in computer graphics, computer vision, and beyond.
Important (References)
[1] Guédon, A., & Lepetit, V. (2023). SuGaR: Surface-Aligned Gaussian Splatting for Efficient 3D Mesh Reconstruction and High-Quality Mesh Rendering. arXiv preprint arXiv:2311.12775.
[2] Huang, B., Yu, Z., Chen, A., Geiger, A., & Gao, S. (2024). 2D Gaussian Splatting for Geometrically Accurate Radiance Fields. SIGGRAPH Conference Papers ‘24.
[3] Kerbl, B., Kopanas, G., Leimkühler, T., & Drettakis, G. (2023). 3D Gaussian Splatting for Real-Time Radiance Field Rendering. ACM SIGGRAPH.
[4] Kazhdan, M., Bolitho, M., & Hoppe, H. (2006). Poisson Surface Reconstruction. Eurographics Symposium on Geometry Processing.
[5] Mildenhall, B., et al. (2020). NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis. ECCV.
Implementation Resources:
